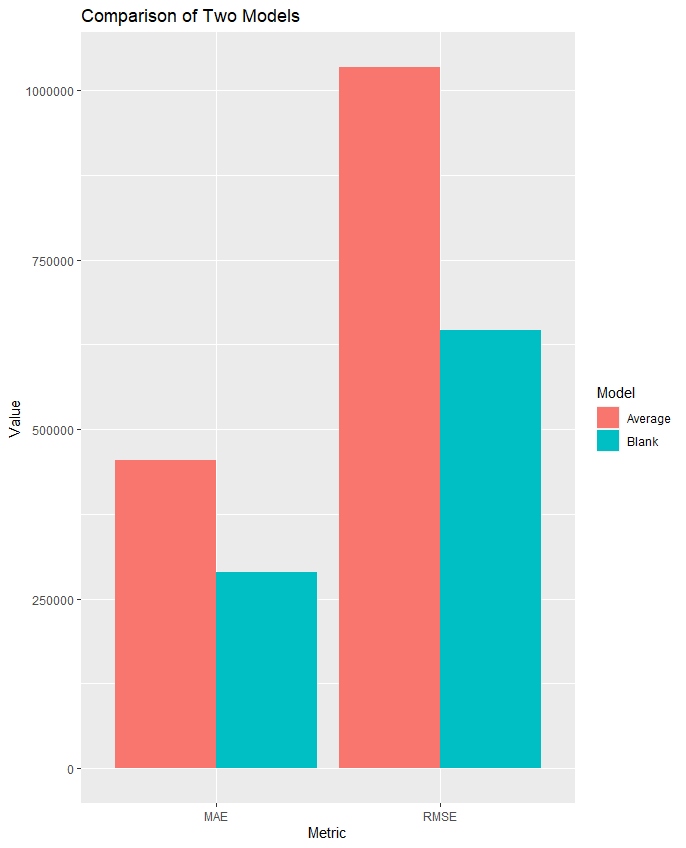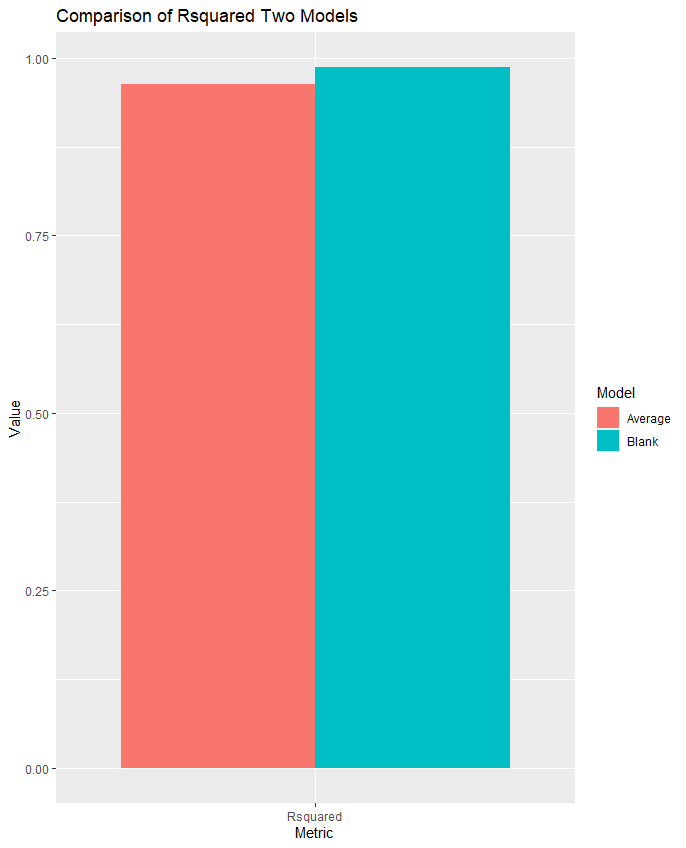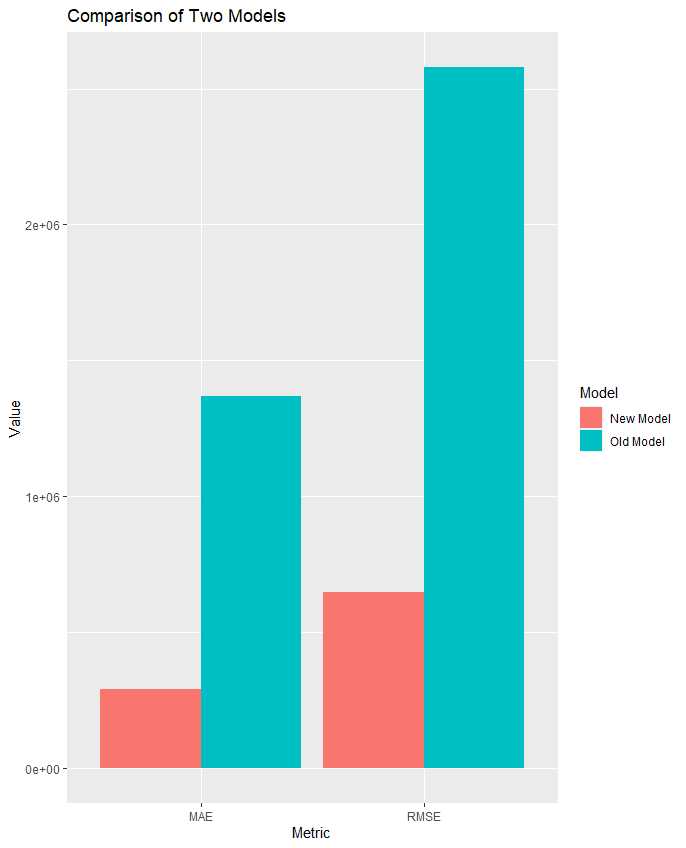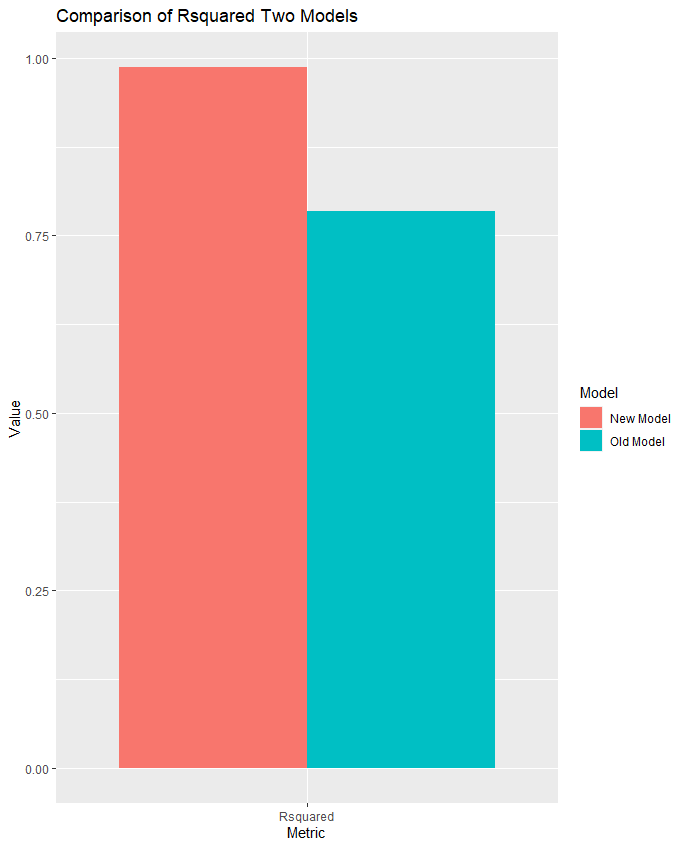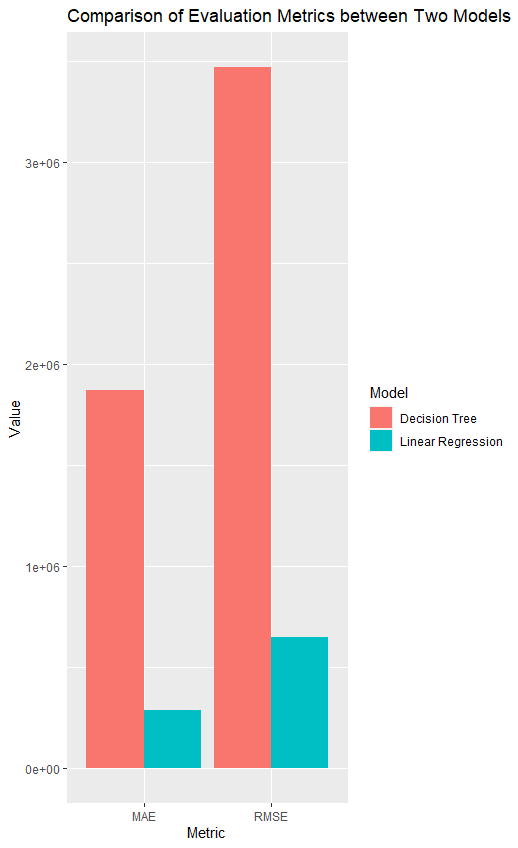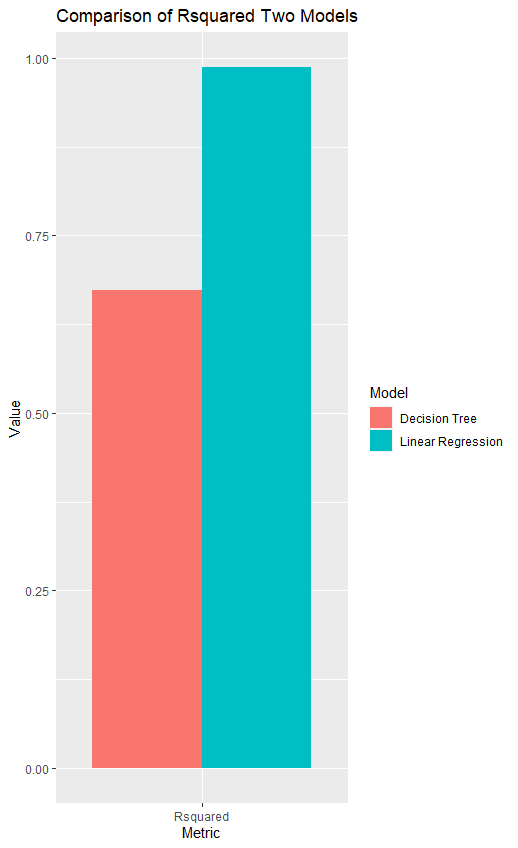准备工作
R语言大作业的要求是这样的:
找到一些公共数据集,下载它们,对它们进行数据分析。
能自己选自己要处理的数据集,那为什么不选点有意思的呢?
第一步的任务是找到合适的公共数据集。在数据科学网站kaggle 上有很多质量非常高的数据集,由衷感谢每一位把自己辛辛苦苦整理好的数据集共享在网站上的数据科学工作者,你们是开源精神的真正践行者,鞠躬。
我最初的设想是找世界杯数据集,分析主客队进球的差异并进行预测,如何进一步推广到比赛的胜负。接着我发现这个思路并不可靠,因为世界杯主客队的区别也就仅限于开球先后的区别,说实话影响不大。更重要的是,世界杯上的比赛随机性非常恐怖,且能挖掘的数据量并不大,都是显而易见的数据,无法深入推进。展开来说,就是足球比赛本身因为过大的随机性导致以我的水平难以建模预测。话说回来,要是任何一种比赛没有随机性,估计也就没人想看了。总之,这导致想水一篇论文的难度变得比较大。
于是我们转变思路,有没有什么整理好的数据,可以量化足球这项运动呢?
答案是足球游戏数值,这是现成的已经量化球员数据。
所以我选用了这个FIFA20数据集 进行建模。EA的FIFA系列年货一年一部,数据更新快,球员数量多,而且结构非常清晰,不需要过多处理就很适合用作建模的数据集。
我的方向是通过球员的数据预测该球员的身价,需要用有逻辑的方法完成建模。
初步建模
处理数据
根据作业要求,我们使用R语言。
拿到一个数据集,第一件事肯定是先看看这个数据集的结构,连数据集里面有什么都不知道还怎么下手?所以我们现在的当务之急就是把刚下好的新鲜数据集导入RStuido进行处理。
查看和设置RStudio的工作路径:
1 2 getwd() setwd("E:/FIFA 20")
如果数据集已经被放在工作路径,可以输入相对路径打开,
1 2 data <- read.csv("FIFA20.csv") data <- read.csv("E:/FIFA 20/FIFA20.csv")
然后导入需要用的包:
1 2 3 4 library(tidyverse) library (corrplot) library(caret) library(rpart)
tidyverse 数据可视化的集成包,包含了ggplot2等包,有助于进行可视化、建模等任务。
corrplot 于绘制相关系数矩阵的 R 包,提供了多种可视化相关系数矩阵的方法。
caret 用于分类、回归和聚类等的包,可以完成数据预处理、特征选择、模型训练、模型评估等任务。
rpart 用于决策树建模的 R 包
在成功导入后,输入下列代码查看数据集基本情况:
由于这个数据集里东西太多,出现了海量的数据,如下:
点击展开/收缩代码块
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 sofifa_id player_url short_name long_name age dob height_cm Min. : 768 Length:18278 Length:18278 Length:18278 Min. :16.00 Length:18278 Min. :156.0 1st Qu.:204446 Class :character Class :character Class :character 1st Qu.:22.00 Class :character 1st Qu.:177.0 Median :226165 Mode :character Mode :character Mode :character Median :25.00 Mode :character Median :181.0 Mean :219739 Mean :25.28 Mean :181.4 3rd Qu.:240796 3rd Qu.:29.00 3rd Qu.:186.0 Max. :252905 Max. :42.00 Max. :205.0 weight_kg nationality club overall potential value_eur wage_eur Min. : 50.00 Length:18278 Length:18278 Min. :48.00 Min. :49.00 Min. : 0 Min. : 0 1st Qu.: 70.00 Class :character Class :character 1st Qu.:62.00 1st Qu.:67.00 1st Qu.: 325000 1st Qu.: 1000 Median : 75.00 Mode :character Mode :character Median :66.00 Median :71.00 Median : 700000 Median : 3000 Mean : 75.28 Mean :66.24 Mean :71.55 Mean : 2484038 Mean : 9457 3rd Qu.: 80.00 3rd Qu.:71.00 3rd Qu.:75.00 3rd Qu.: 2100000 3rd Qu.: 8000 Max. :110.00 Max. :94.00 Max. :95.00 Max. :105500000 Max. :565000 player_positions preferred_foot international_reputation weak_foot skill_moves work_rate body_type Length:18278 Length:18278 Min. :1.000 Min. :1.000 Min. :1.000 Length:18278 Length:18278 Class :character Class :character 1st Qu.:1.000 1st Qu.:3.000 1st Qu.:2.000 Class :character Class :character Mode :character Mode :character Median :1.000 Median :3.000 Median :2.000 Mode :character Mode :character Mean :1.103 Mean :2.944 Mean :2.368 3rd Qu.:1.000 3rd Qu.:3.000 3rd Qu.:3.000 Max. :5.000 Max. :5.000 Max. :5.000 real_face release_clause_eur player_tags team_position team_jersey_number loaned_from joined Length:18278 Min. : 13000 Length:18278 Length:18278 Min. : 1.0 Length:18278 Length:18278 Class :character 1st Qu.: 563000 Class :character Class :character 1st Qu.: 9.0 Class :character Class :character Mode :character Median : 1200000 Mode :character Mode :character Median :17.0 Mode :character Mode :character Mean : 4740717 Mean :20.1 3rd Qu.: 3700000 3rd Qu.:27.0 Max. :195800000 Max. :99.0 NA's :1298 NA's :240 contract_valid_until nation_position nation_jersey_number pace shooting passing dribbling Min. :2019 Length:18278 Min. : 1.00 Min. :24.0 Min. :15.0 Min. :24.00 Min. :23.00 1st Qu.:2020 Class :character 1st Qu.: 6.00 1st Qu.:61.0 1st Qu.:42.0 1st Qu.:50.00 1st Qu.:57.00 Median :2021 Mode :character Median :12.00 Median :69.0 Median :54.0 Median :58.00 Median :64.00 Mean :2021 Mean :12.12 Mean :67.7 Mean :52.3 Mean :57.23 Mean :62.53 3rd Qu.:2022 3rd Qu.:18.00 3rd Qu.:75.0 3rd Qu.:63.0 3rd Qu.:64.00 3rd Qu.:69.00 Max. :2026 Max. :30.00 Max. :96.0 Max. :93.0 Max. :92.00 Max. :96.00 NA's :240 NA's :17152 NA's :2036 NA's :2036 NA's :2036 NA's :2036 defending physic gk_diving gk_handling gk_kicking gk_reflexes gk_speed gk_positioning Min. :15.00 Min. :27.00 Min. :44.00 Min. :42.00 Min. :35.00 Min. :45.00 Min. :12.0 Min. :41.00 1st Qu.:36.00 1st Qu.:59.00 1st Qu.:60.00 1st Qu.:58.00 1st Qu.:57.00 1st Qu.:60.75 1st Qu.:29.0 1st Qu.:58.00 Median :56.00 Median :66.00 Median :65.00 Median :63.00 Median :61.00 Median :66.00 Median :39.0 Median :64.00 Mean :51.55 Mean :64.88 Mean :65.42 Mean :63.15 Mean :61.83 Mean :66.39 Mean :37.8 Mean :63.38 3rd Qu.:65.00 3rd Qu.:72.00 3rd Qu.:70.00 3rd Qu.:68.00 3rd Qu.:66.00 3rd Qu.:72.00 3rd Qu.:46.0 3rd Qu.:69.00 Max. :90.00 Max. :90.00 Max. :90.00 Max. :92.00 Max. :93.00 Max. :92.00 Max. :65.0 Max. :91.00 NA's :2036 NA's :2036 NA's :16242 NA's :16242 NA's :16242 NA's :16242 NA's :16242 NA's :16242 #数据过多,部分展示,下略。
我们只需要取到部分有用的即可,大部分无意义的数据(例如player_url等)并不需要考虑。
所以我们现在的任务是整理数据,把有用的部分从完整的数据集里取出,单独组合在一起,这样有利于更方便地训练我们的模型。
初步考虑后,我挑选了以下数据:
‘height_cm’,‘weight_kg’ 身高、体重的基本信息
‘skill_moves’,‘pace’,‘shooting’,‘passing’,‘dribbling’,‘defending’,‘physic’ 传球,射门等技术水平
‘gk_diving’,‘gk_handling’,‘gk_kicking’,‘gk_reflexes’,‘gk_speed’,‘gk_positioning’ 门将技术水平
‘overall’,‘potential’,‘wage_eur’ 能力值,潜力,年薪等参考数值
‘value_eur’ 身价本身,用于训练的最关键数据
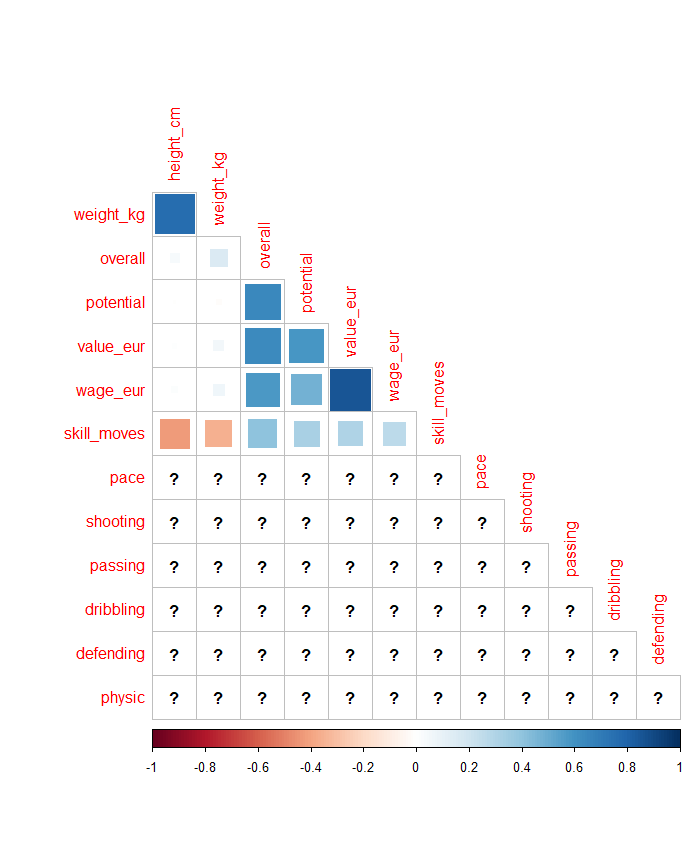
接下来,出于逻辑性的考虑,我们应该优先对这些数据进行初步的相关性分析。
如果直接处理这些数据,会出现一个问题:部分内容无法被正确分析,显示出问号。
根据对图像中出错区域的分析,这可能是由于数据缺失导致的。
在这里我优先怀疑是否存在数据集质量较低,数据不完全的情况。
输入代码如下查看球员传球这一项的数据:
1 2 head (short_name) head (passing)
得到结果如下:
1 2 3 4 5 > head (short_name) [1] "L. Messi" "Cristiano Ronaldo" "Neymar Jr" "J. Oblak" [5] "E. Hazard" "K. De Bruyne" > head (passing) [1] 92 82 87 NA 86 92
在返回结果中,我们发现 "J. Oblak"这位球员没有’‘passing’'数据,因为奥布拉克是效力于马德里竞技的门将。作为门将,他在游戏里的任务只是守门,只有门将特有的部分属性。他并没有被设置传球数据,所以这一项设为NA,如果直接对数据进行处理就会出现不可避免的错误。
同理,梅西也不会有’‘gk_positioning’'数据,因为他根本不会守门,也不会有门将站位的数据,如果直接对他进行处理,也会在门将的数据上出相同的错。
对于这个问题,我的解决方案是把门将和非门将球员区分开,因为这两个位置的量化数据是不一样的。
所以我给出代码如下:
1 2 3 4 5 6 7 8 9 10 11 #处理非门将有效数据,无关紧要的数据去除 data <- df[,c('height_cm','weight_kg','overall','potential','value_eur','release_clause_eur','wage_eur','skill_moves','pace','shooting','passing','dribbling','defending','physic')] data <- data[!is.na(data$passing),] #守门员没有passing数据,这一行去掉所有passing为NA的球员 corr_matrix <- cor(data) corrplot(corr_matrix, method = "square",diag = F, type = "lower") #处理非门将有效数据,无关紧要的数据去除 data_gk <- df[,c('height_cm','weight_kg','overall','potential','value_eur','release_clause_eur','wage_eur','gk_diving','gk_handling','gk_kicking','gk_reflexes','gk_speed','gk_positioning')] data_gk <- data_gk[!is.na(data_gk$gk_diving),] #同上,筛选门将。 corr_matrix_gk <- cor(data_gk) corrplot(corr_matrix_gk, method = "square",diag = F, type = "lower")
这段代码筛选了门将球员和非门将球员,为他们各自保留了有价值的数据。
cor()函数用于计算变量之间的相关系数,生成一个由变量之间的相关性组成的方阵,其中对角线上的元素表示每个变量与自身之间的相关性(始终为1),而非对角线的元素则表示每对变量之间的相关性。
corrplot()函数用于创建相关性矩阵的图。method = "square"参数指定图应该是方形的,diag = F参数则指示函数从绘图中删除对角线元素(因为它们始终为1)。最后,type = "lower"参数指定只显示相关性矩阵的下三角部分,因为矩阵是对称的,上三角部分是重复的。
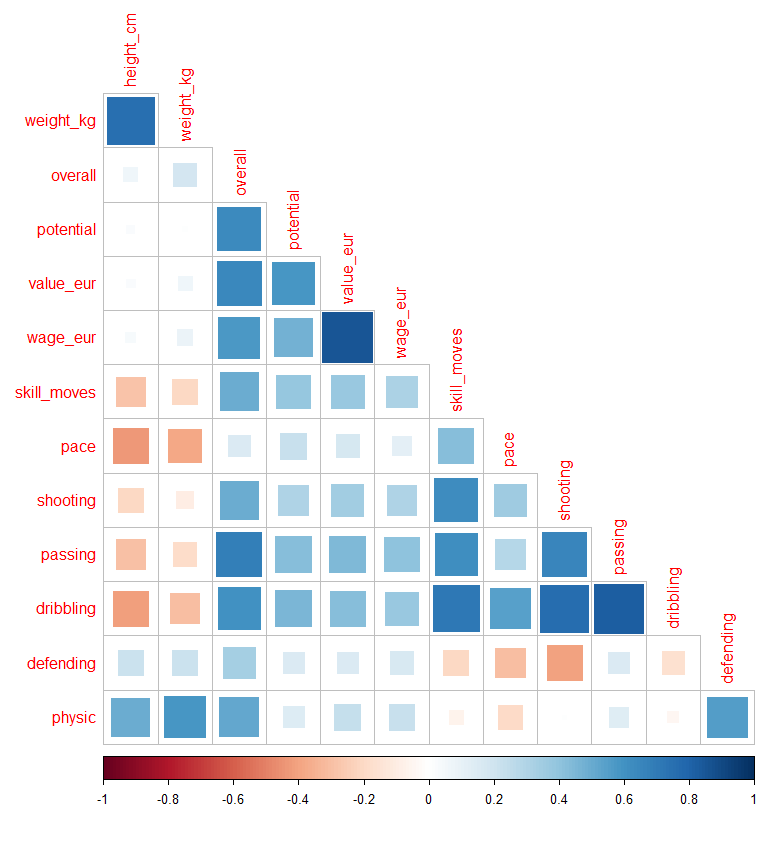
可视化结果为下图:
越蓝的部分相关性越强,越红的部分相关性越弱。
不难发现所有选中的数据与身价 'value_eur’的交点都是蓝色,正相关。
用线性回归模型建模
现在开始建模,我先选用线性回归模型,对非门将球员进行处理。
首先需要把数据拆分为训练集和实验集,在训练集训练模型后,用实验集的数据去测试模型,这样可以有效评估模型精度。我们把数据拆分成70%训练集,30%实验集。
为了让结果可复现,还需要设置一个种子保证在这个种子下的每次随机生成结果都一样。
代码如下:
1 2 3 4 set.seed(313) ind <- sample(2,nrow(data),replace=T,prob=c(0.7,0.3)) data_train <- data[ind == 1,] data_test <- data[ind == 2,]
这段代码用于将一个数据集 data 划分为训练集和测试集。
具体来说,set.seed(313) 是设置一个随机种子,以确保每次运行代码时都能得到相同的随机结果。ind <- sample(2,nrow(data),replace=T,prob=c(0.7,0.3)) 则是生成一个长度为 nrow(data)的随机数向量,其中每个元素的取值为 1 或 2,概率分别为 0.7 和 0.3,表示将数据集中的样本随机划分为训练集和测试集。其中,sample() 函数用于生成随机数向量,replace=T 表示采样时可以重复抽样,prob=c(0.7,0.3) 表示生成的随机数向量中取值为 1 和 2的概率分别为 0.7 和 0.3。
接下来,data_train <- data[ind == 1,] 将数据集中随机取值为 1的样本作为训练集,赋值给 data_train 变量。而 data_test <- data[ind == 2,] 则将数据集中随机取值为 2的样本作为测试集,赋值给 data_test 变量。
通过将数据集划分为训练集和测试集,我们可以使用训练集来训练模型,并使用测试集来评估模型的性能。这样可以更好地估计模型对未知数据的预测能力,并避免模型在训练数据上过拟合的问题。
接下来,把数据导入,得到模型data_model。
1 data_model <- lm(value_eur~ height_cm + weight_kg + overall + potential + wage_eur + skill_moves + pace + shooting + passing + dribbling + defending + physic,data_train)
接下来使用这个模型,对测试集里的数据进行预测,用data_pred接收预测的结果。
1 data_pred = predict(data_model,data_test)
为了有效评估模型的准确度,我们用真实值减去预测值得到误差data_error。
1 2 data_actual <- data_test$value_eur data_error <- data_actual - data_pred
误差可视化分析
接下来,我们对误差进行可视化处理。
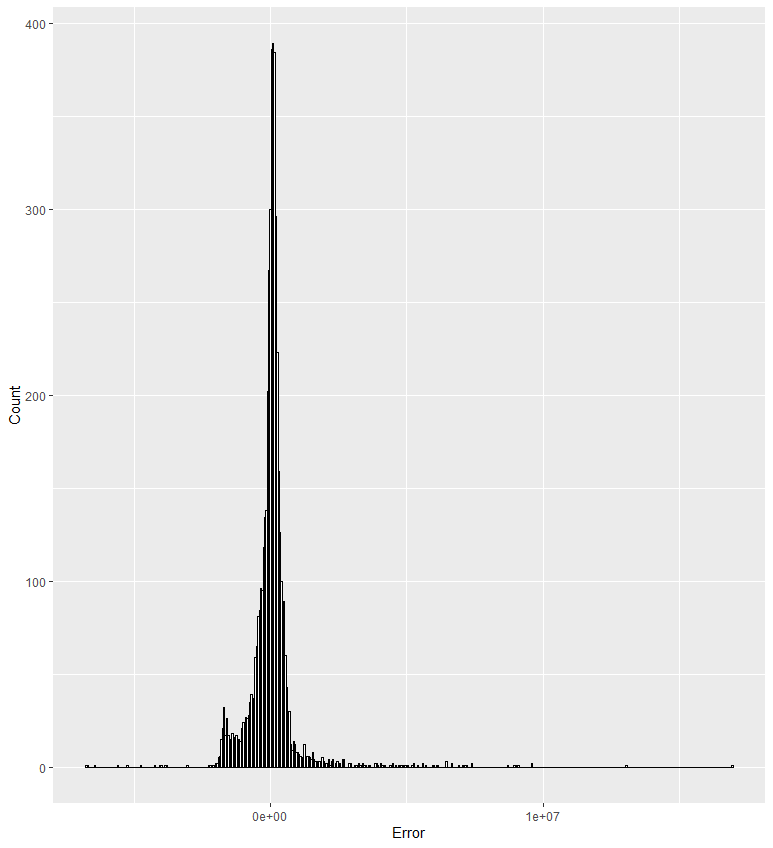
如果直接画图,会出现这样的结果:
这不是能获取有效信息的图。显然x轴范围太大了,是部分极端数据导致的。
反复试错后,确定范围为±1500000,这样的图牺牲了304个极端数据。而测试集样本总量为4851个,去除了约6%的数据,我认为这是可以接受的误差。
代码如下:
1 2 3 4 5 ggplot(data.frame(data_error), aes(x = data_error, fill = (data_error > 0))) + geom_histogram(binwidth = 50000, color = "black") + scale_x_continuous(limits = c(-1500000, 1500000)) + scale_fill_manual(values = c("red", "green")) + # 手动指定颜色 xlab("Error") + ylab("Count")
具体来说,data.frame(data_error) 将一个包含模型误差的向量 data_error 转换为数据框(data frame)格式,并将其作为 ggplot() 函数的数据源。aes(x = data_error, fill = (data_error > 0)) 则指定了直方图的变量和填充颜色,其中 x 参数指定了直方图的横轴变量为 data_error,而 fill 参数则根据 data_error的取值是否大于 0 来填充直方图的颜色。
接下来,geom_histogram(binwidth = 50000, color = “black”) 添加了一个直方图层,其中 binwidth 参数指定了直方图的柱宽为 50000,color 参数指定了柱子的边框颜色为黑色。
scale_x_continuous(limits = c(-1500000, 1500000)) 和 scale_fill_manual(values = c(“red”, “green”)) 分别指定了直方图横轴的取值范围和填充颜色的取值范围。其中,limits 参数将横轴的取值范围限制在 -1500000 到 1500000 之间,values 参数手动指定了填充颜色为红色和绿色。
最后,xlab(“Error”) + ylab(“Count”) 分别指定了横轴和纵轴的标签为 “Error” 和 “Count”。
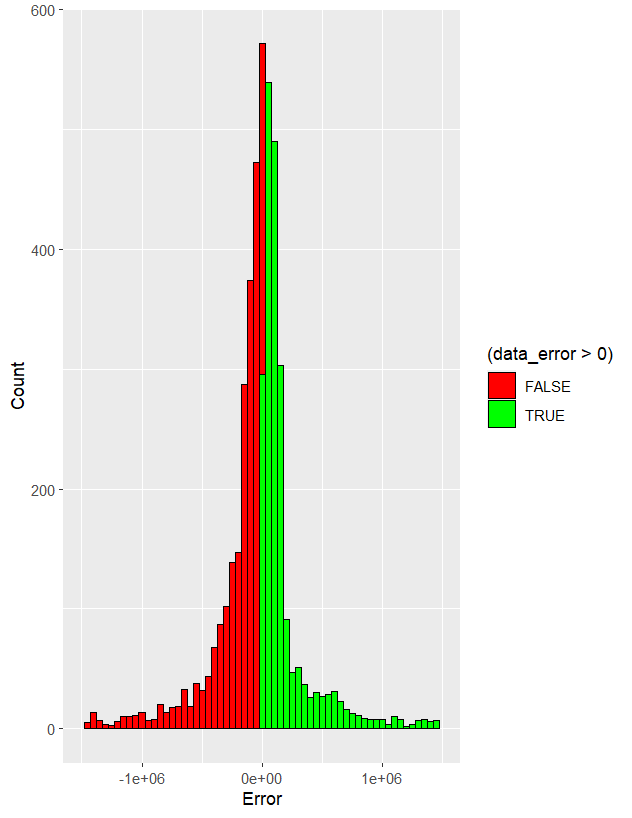
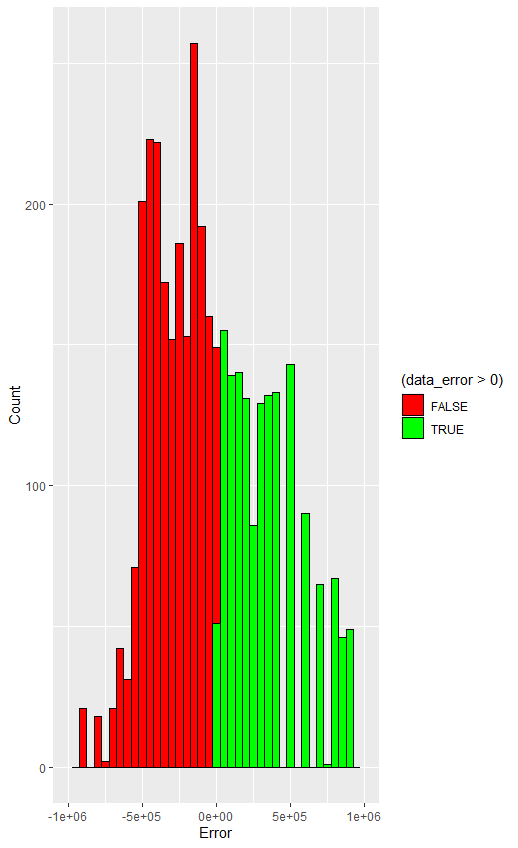
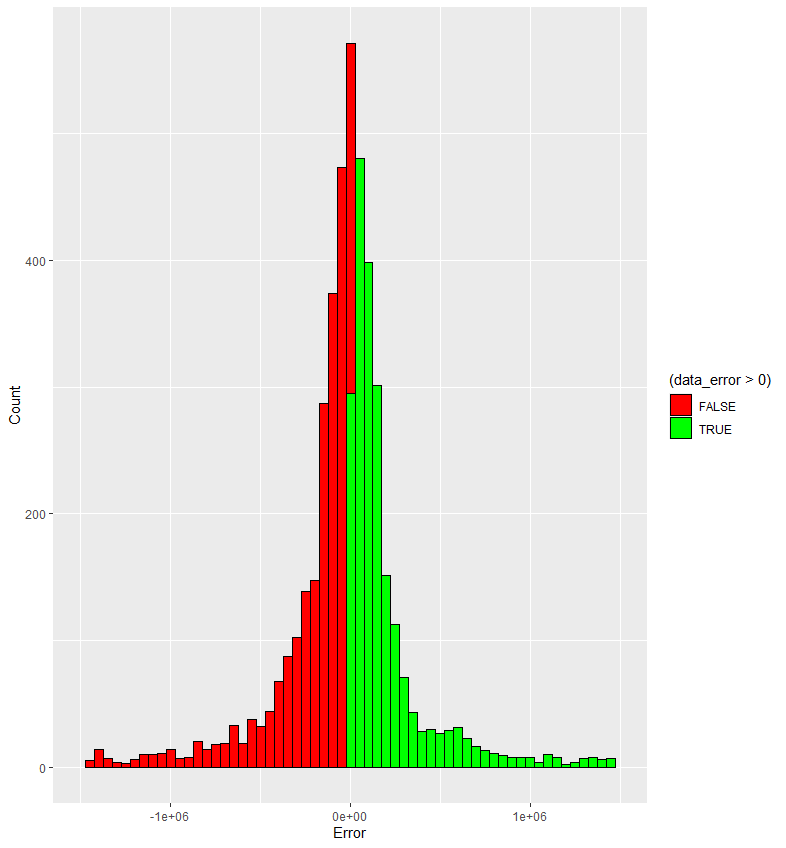
画出的图像如下:
可见大体符合正态分布的形式。
接下来绘制残差图,代码如下:
1 2 plot(data_pred, data_error, xlab = "Predicted Value", ylab = "Residuals", xlim = c(-1000000, 1000000),ylim = c(-3000000, 3000000)) abline(h = 0, col = "red")
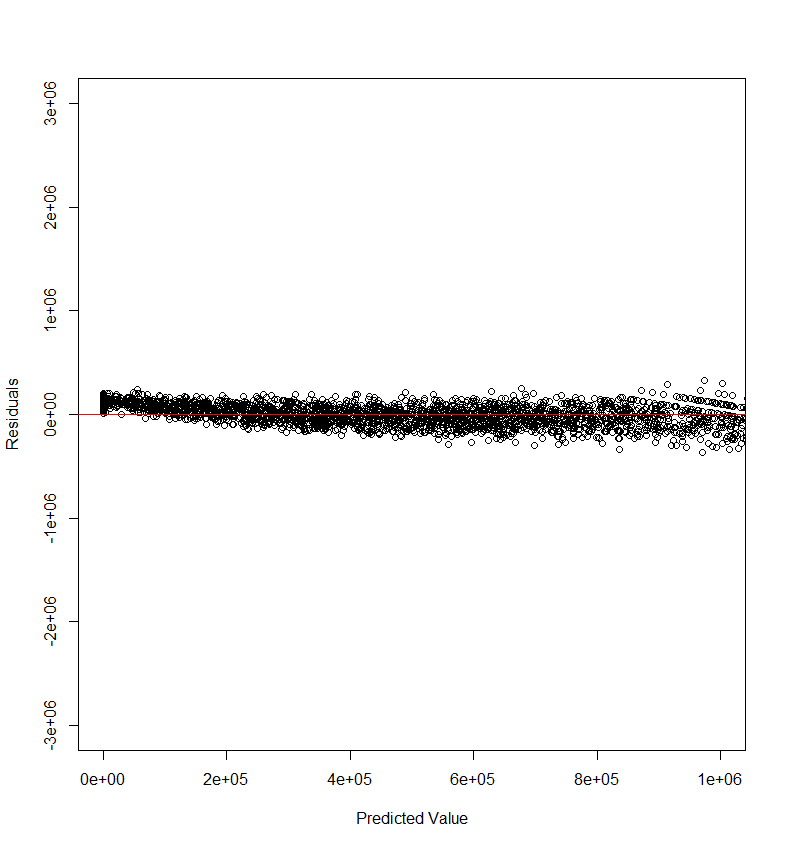
图像如下:
发现左侧误差普遍较高,通常意味着模型在预测较小的变量时出现了偏差。可是这里,模型居然给出了小于0的预测值,这是不可接受的,我们需要用ifelse语句修正。
补充代码如下:
1 data_pred <- ifelse(data_pred<0,0,data_pred)
接下来使用交叉验证,代码如下:
1 2 3 4 5 6 # 创建一个交叉验证控制对象ctrl,指定交叉验证方法为"cv",即k折交叉验证,k的值为10。 ctrl <- trainControl(method = "cv", number = 10) # 进行交叉验证 data_model_cv1 <- train(value_eur ~., data = data_train, method = "lm",trControl = ctrl) # 查看交叉验证结果 data_model_cv1$results
这里使用的k折交叉验证是其中最常用的一种。它将数据集分成k个大小相等的子集,然后重复k次。在每一次重复中,选择其中一个子集作为测试集,其余的k-1个子集作为训练集。然后对模型进行训练,并在测试集上进行测试,记录误差。这样就会得到k个评估分数,平均值可以作为模型的性能指标。这种方法可以有效地减少模型过拟合和欠拟合的可能性,从而提高模型的泛化能力。
得出结果:
1 2 intercept RMSE Rsquared MAE RMSESD RsquaredSD MAESD 1 TRUE 2578957 0.7844251 1370050 316320 0.03640009 60225.02
术语笔记记录:
RMSE(Root Mean Squared Error):均方根误差,是实际值与预测值之间误差的平方和的平均值的平方根。RMSE越小,代表模型的预测能力越好。
R-squared(R平方):决定系数,是实际值与预测值之间的相关性的平方。R平方在0到1之间,越接近1代表模型的拟合程度越好。
MAE(Mean Absolute Error):平均绝对误差,是实际值与预测值之间误差的绝对值的平均值。MAE越小,代表模型的预测能力越好。
RMSESD:RMSE的标准差,用于评估模型的泛化能力。
RsquaredSD:R平方的标准差,用于评估模型的稳定性。
MAESD:MAE的标准差,用于评估模型的稳定性和泛化能力。
R值仅有0.78,均方根误差2578957,平均绝对误差1370050。
可以接受,我们仍然能做得更好。
误差分析和修正
采用数据的问题
上文提及,我采用了如下的数据。
‘height_cm’,‘weight_kg’ 身高、体重的基本信息
‘skill_moves’,‘pace’,‘shooting’,‘passing’,‘dribbling’,‘defending’,‘physic’ 传球,射门等技术水平
‘gk_diving’,‘gk_handling’,‘gk_kicking’,‘gk_reflexes’,‘gk_speed’,‘gk_positioning’ 门将技术水平
‘overall’,‘potential’,‘wage_eur’ 能力值,潜力,年薪等参考数值
‘value_eur’ 身价本身,用于训练的最关键数据
这些数据是否完全反映了球员的身价?基本信息已经完全录入,而还可以入手的地方就是侧面反映球员能力的’‘参考数据’'。除能力值,潜力,年薪之外,我发现我在第一轮建模时忽略了一个数据:强制解约金。
其他球队可以通过支付这笔解约金来买断这名球员的合同,解约金一般高于该球员身价。数据集里梅西的解约金是1.9亿欧元,而某位不知名球员’‘Mohammed Sagaf’'解约金只有可怜的7万欧元。所以我认为,球员的合同里存在的强制解约金可以间接反映这个球员的价值。
在训练模型时加入解约金这一项,代码如下:
1 2 3 4 data <- df[,c('height_cm','weight_kg','overall','potential','value_eur','release_clause_eur','wage_eur','skill_moves','pace','shooting','passing','dribbling','defending','physic')] data <- data[!is.na(data$passing),] #守门员没有passing数据 corr_matrix <- cor(data) corrplot(corr_matrix, method = "square",diag = F, type = "lower")
如果直接处理,仍然会出现问号,如下图:
检查数据集,代码如下:
1 summary(data$release_clause_eur)
结果如下:
1 2 Min. 1st Qu. Median Mean 3rd Qu. Max. NA's 18000 609000 1300000 4924714 4000000 195800000 1165
可见1165个球员的合同并没有加入解约金条款,所以解约金数据空缺。
现在有两个方法处理这些空缺的数据:
去除所有空缺数据。
把空缺的部分用该项数据的平均值填补。
这部分球员数量占比仅达到了7%左右,且水平参差不齐,用该项数据的平均值填补可能导致出现进一步的误差。处于严谨性,我们按之前建立线性回归模型的方法对这两种方法都进行一次测试,量化地对比两个方法。
去除所有空缺数据
与先前的方法相比,添加代码如下:
1 data <- data[!is.na(data$release_clause_eur),]
这个代码可以把所有空缺项全部去掉,接下来按之前的方法操作,最后再使用交叉验证。
1 2 3 4 5 6 # 创建一个交叉验证控制对象ctrl,指定交叉验证方法为"cv",即k折交叉验证,k的值为10。 ctrl <- trainControl(method = "cv", number = 10) # 进行交叉验证 data_model_cv1 <- train(value_eur ~., data = data_train, method = "lm",trControl = ctrl) # 查看交叉验证结果 data_model_cv1$results
得出结果:
1 2 intercept RMSE Rsquared MAE RMSESD RsquaredSD MAESD 1 TRUE 646712.3 0.9867474 289196.5 57692.47 0.00225056 11995.83
可以发现,这里已经比原模型有了较明显的提升,在分析出更好的处理方法后,我们会对它们的结果进行可视化处理,有利于直观地分析差距。
用平均值填补
与先前的方法相比,添加代码如下:
1 data$release_clause_eur[is.na(data$release_clause_eur)] <- mean(data$release_clause_eur, na.rm = TRUE)
这个把所有空缺项全部用解约金平均值填补。接下来按之前的方法操作,最后再使用交叉验证。
1 2 3 4 5 6 # 创建一个交叉验证控制对象ctrl,指定交叉验证方法为"cv",即k折交叉验证,k的值为10。 ctrl <- trainControl(method = "cv", number = 10) # 进行交叉验证 data_model_cv1 <- train(value_eur ~., data = data_train, method = "lm",trControl = ctrl) # 查看交叉验证结果 data_model_cv1$results
得出结果:
1 2 intercept RMSE Rsquared MAE RMSESD RsquaredSD MAESD 1 TRUE 1034079 0.9633106 454096.9 322250.3 0.022778 31027.41
可视化分析
评估思路非常简单,对比两组数据即可。首先把两组数据单独列出,代码如下:
1 2 df1 <- as.data.frame(data_model_cv1$results) df2 <- as.data.frame(data_model_cv2$results)
这段代码将 data_model_cv1 和 data_model_cv2 两个交叉验证模型的结果转换为数据框(data frame)格式,并分别赋值给了 df1 和 df2 两个变量。
先合并RMSE/MAE数据,因为它们相近且远大于R方。然后绘图。代码如下:
1 2 3 4 5 6 7 8 9 # 合并RMSE/MAE df <- data.frame(Model = rep(c("Blank", "Average"), each = 2), Metric = rep(c("RMSE", "MAE"), 2), Value = c(df1$RMSE,df1$MAE, mean(df2$RMSE),mean(df2$MAE))) # 绘制关于RMSE/MAE的柱状图 ggplot(df, aes(x = Metric, y = Value, fill = Model)) + geom_bar(stat = "identity", position = position_dodge()) + labs(title = "Comparison of Two Models", x = "Metric", y = "Value", fill = "Model")
同理处理R方,代码如下:
1 2 3 4 5 6 7 8 9 # 合并数据框,R方 df <- data.frame(Model = rep(c("Blank", "Average"), each = 1), Metric = rep(c('Rsquared'), 2), Value = c(df1$Rsquared,mean(df2$Rsquared))) # 绘制关于R方的柱状图 ggplot(df, aes(x = Metric, y = Value, fill = Model)) + geom_bar(stat = "identity", position = position_dodge()) + labs(title = "Comparison of Rsquared Two Models", x = "Metric", y = "Value", fill = "Model")
得到的图像是:
可以清晰看出,“去除所有空缺数据”这一方法效果更好。
我们就采用这种方法建模。
空缺数据的问题
虽然我们解决了门将和非门将的能力值不同导致的问题,但是数据是否真的没有空缺仍然需要对数据集进行进一步的检查和分析。我在对最关键的数据‘value_eur’,即身价本身检查时发现了问题,代码如下:
检查结果如下:
1 2 Min. 1st Qu. Median Mean 3rd Qu. Max. 0 325000 700000 2484038 2100000 105500000
可见身价的最低值是0,而我们的问题是:球员身价为0是否是建模时的可靠依据?
继续挖掘数据,查看身价为0的球员到底有哪些。代码如下:
1 data[data$value_eur == 0,]
输出结果如下:
点击展开/收缩代码块
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 height_cm weight_kg overall potential value_eur wage_eur skill_moves pace shooting passing 328 185 80 82 82 0 0 2 80 43 56 329 177 75 82 82 0 0 4 81 77 81 408 181 82 81 81 0 0 2 71 61 57 409 171 63 81 81 0 0 4 82 72 77 410 188 83 81 81 0 0 3 80 82 60 411 188 84 81 81 0 0 4 80 80 56 567 177 75 80 80 0 0 3 68 62 74 568 178 69 80 80 0 0 4 79 54 76 750 182 79 79 79 0 0 2 70 48 60 751 175 70 79 79 0 0 2 81 57 72 753 176 73 79 79 0 0 4 84 79 65 792 179 71 78 83 0 0 3 73 38 65 802 175 70 78 82 0 0 3 75 73 76 869 180 78 78 78 0 21000 3 36 51 67 889 183 80 78 78 0 0 2 59 49 64 918 196 91 78 78 0 0 3 65 76 67 990 168 65 78 78 0 0 4 87 58 70 991 177 75 78 78 0 0 3 78 51 69 992 174 71 78 78 0 0 4 80 73 76 1088 182 74 77 80 0 0 3 80 68 73 1161 184 74 77 77 0 0 3 73 76 63 1250 188 88 77 77 0 0 3 71 70 69 1251 178 71 77 77 0 0 4 80 68 77 1252 176 75 77 77 0 0 4 80 71 71 #截取部分,下略。
在输出结果里,存在大量能力值并不低的球员,他们的身价不应该为0。
对照数据集检查,在这份名单里出现的球员在那时都没有合同,正好处于自由身状态。换句话说,这个数据集里的自由球员身价都为0,这导致了误差的出现,所以我们需要处理自由身球员的身价。
我采取的方法是去除所有的自由球员,因为自由球员的数量并不大,仅有134个,比3.1中更少。而上面已经说明,去除所有自由球员效果更好。
代码如下:
1 data_gk <- data_gk[!('value_eur' == 0),] #自由球员身价是0,无参考价值,应该去掉
接下来按之前的方法评估模型,输出如下:
1 2 intercept RMSE Rsquared MAE RMSESD RsquaredSD MAESD 1 TRUE 2602833 0.7828398 1377350 224113.4 0.02685402 70124.29
效果并不比原模型好多少,几乎一致。
合二为一
综上,我们的建模的代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 #按“去除所有空缺数据”处理球员数据,相比“赋予平均值”效果更好,接下来会证明 data <- df[,c('height_cm','weight_kg','overall','potential','value_eur','release_clause_eur','wage_eur','skill_moves','pace','shooting','passing','dribbling','defending','physic')] data <- data[!is.na(data$passing),] #守门员没有passing数据,精准打击 data <- data[!is.na(data$release_clause_eur),] #分训练集和实验集 set.seed(313) ind <- sample(2,nrow(data),replace=T,prob=c(0.7,0.3)) data_train <- data[ind == 1,] data_test <- data[ind == 2,] #建模 data_model <- lm(value_eur~ height_cm + weight_kg + overall + release_clause_eur + potential + wage_eur + skill_moves + pace + shooting + passing + dribbling + defending + physic,data_train) #获取误差 data_pred = predict(data_model,data_test) data_pred <- ifelse(data_pred<0,0,data_pred) data_actual <- data_test$value_eur data_error <- data_actual - data_pred
输出代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 # 将评估结果单独列出 df1 <- as.data.frame(data_model_cv1$results) df2 <- as.data.frame(data_model_cv2$results) # 合并RMSE/MAE df <- data.frame(Model = rep(c("New Model","Old Model"), each = 2), Metric = rep(c("RMSE", "MAE"), 2), Value = c(df1$RMSE,df1$MAE, mean(df2$RMSE),mean(df2$MAE))) # 绘制关于RMSE/MAE的柱状图 ggplot(df, aes(x = Metric, y = Value, fill = Model)) + geom_bar(stat = "identity", position = position_dodge()) + labs(title = "Comparison of Two Models", x = "Metric", y = "Value", fill = "Model") # 合并数据框,R方 df <- data.frame(Model = rep(c( "New Model","Old Model"), each = 1), Metric = rep(c('Rsquared'), 2), Value = c(df1$Rsquared,mean(df2$Rsquared))) # 绘制关于R方的柱状图 ggplot(df, aes(x = Metric, y = Value, fill = Model)) + geom_bar(stat = "identity", position = position_dodge()) + labs(title = "Comparison of Rsquared Two Models", x = "Metric", y = "Value", fill = "Model")
结果是:
1 2 intercept RMSE Rsquared MAE RMSESD RsquaredSD MAESD 1 TRUE 646712.3 0.9867474 289196.5 57692.47 0.00225056 11995.83
去除自由球员后,模型精度并未变化。
现在的模型和原模型对比如下:
好,那现在我的评价是:薄纱。
与决策树模型对比
决策树模型建模
决策树模型的建立过程与线性回归模型很像,我们导入的数据保持先前发现的最好配置,即“去除自由球员”,“去除无解约金球员”。这样不仅保证了模型精度,也和线性回归模型一致。
建模过程的代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 # 划分训练集和测试集 set.seed(313) ind <- sample(2, nrow(data), replace = TRUE, prob = c(0.7, 0.3)) data_train <- data[ind == 1, ] data_test <- data[ind == 2, ] # 构建决策树模型 data_model <- rpart(value_eur ~ height_cm + weight_kg + overall + release_clause_eur + potential + wage_eur + skill_moves + pace + shooting + passing + dribbling + defending + physic, data = data_train) # 对测试集进行预测 data_pred <- predict(data_model, data_test) data_pred <- ifelse(data_pred<0,0,data_pred) # 计算预测误差 data_actual <- data_test$value_eur data_error <- data_actual - data_pred
误差可视化分析
同理,代码如下:
1 2 3 4 5 6 7 # 绘制误差直方图,限制误差范围为±1000000 ggplot(data.frame(data_error), aes(x = data_error, fill = (data_error > 0))) + geom_histogram(binwidth = 50000, color = "black") + scale_x_continuous(limits = c(-1000000, 1000000)) + scale_fill_manual(values = c("red", "green")) + xlab("Error") + ylab("Count")
得到图像如下:
看起来略抽象。
与线性回归模型对比
代码与3.1近似,需要注意的是,决策树模型使用交叉验证得到了三组结果,需要用平均值处理。如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 # 将评估结果转换为数据框 df1 <- as.data.frame(data_model_cv1$results) df2 <- as.data.frame(data_model_cv2$results) # 合并数据框,RMSE/MAE df <- data.frame(Model = rep(c("Linear Regression", "Decision Tree"), each = 2), Metric = rep(c("RMSE", "MAE"), 2), Value = c(df1$RMSE,df1$MAE, mean(df2$RMSE),mean(df2$MAE))) # 绘制关于RMSE/MAE的柱状图 ggplot(df, aes(x = Metric, y = Value, fill = Model)) + geom_bar(stat = "identity", position = position_dodge()) + labs(title = "Comparison of Evaluation Metrics between Two Models", x = "Metric", y = "Value", fill = "Model") # 合并数据框,R方 df <- data.frame(Model = rep(c("Linear Regression", "Decision Tree"), each = 1), Metric = rep(c('Rsquared'), 2), Value = c(df1$Rsquared,mean(df2$Rsquared))) # 绘制关于R方的柱状图 ggplot(df, aes(x = Metric, y = Value, fill = Model)) + geom_bar(stat = "identity", position = position_dodge()) + labs(title = "Comparison of Rsquared Two Models", x = "Metric", y = "Value", fill = "Model")
得到图像如下:
甚至不如原模型,决策树你就是逊啊。
建模总结
最终,我的模型效果如下:
1 2 intercept RMSE Rsquared MAE RMSESD RsquaredSD MAESD 1 TRUE 646712.3 0.9867474 289196.5 57692.47 0.00225056 11995.83
预测误差直方图:
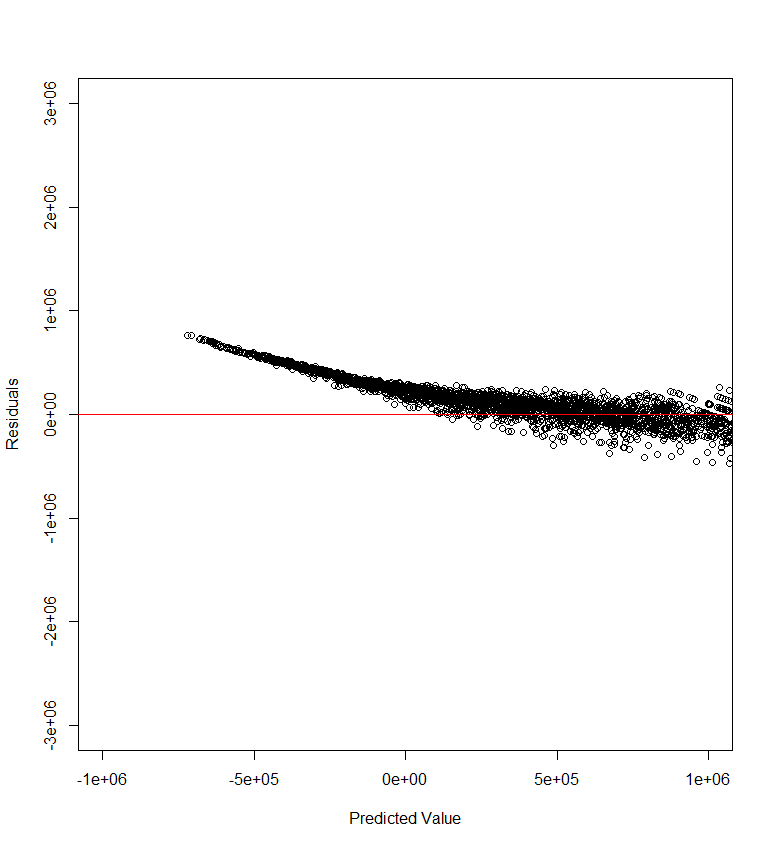
残差图:
可见已经较为贴近直线,拟合效果较好。
建模工作结束,关山难越今日越。